A Rotation Invariant Latent Factor Model for Moveme Discovery from Static Poses ICDM'16
Introduction
What are the typical ranges of motion for human arms? What types of leg movements tend to correlate with specific shoulder positions? How can we expect the arms to move given the current body pose? Our goal is to address these questions by recovering a set of ``bases poses'' that summarize the variability of movements in a given collection of static poses captured from images at various viewing angles.
One of the main difficulties of studying human movement is that it is a priori unrestricted, except for physically imposed joint angle limits which have been studied in medical text books, typically for a limited number of configurations. Furthermore, human movement may be distinguished into movemes, actions, and activities depending on structure, complexity, and duration. Movemes refer to the simplest meaningful pattern of motion: a short, target-oriented trajectory, that cannot be further decomposed, e.g. ``reach'', ``grasp'', ``step'', ``kick''.
Extensive studies have been carried out on human action and activity recognition, however little attention has been paid to movemes since human behaviour is difficult to analyze at such a fine scale of dynamics. In this paper, our primary goal is to learn a basis space to smoothly capture movemes from a collection of two dimensional images, although our learned representation can also aid in higher level reasoning.

Contributions
Given a collection of static joint locations from images taken at any angle of view we learn a factorization into a basis pose matrix U and a coefficient matrix V. The learned basis poses U are rotation-invariant and can be globally applied across a range of viewing angles. A sparse linear combination of the learned basis accurately reconstructs the pose of a human involved in an action at any angle of view, also for poses not contained in the training set. In summary, the main contributions of our paper are:
-
An unsupervised method for learning a rotation-invariant set of basis poses. We propose a solution to the intrinsically ill-posed problem of going from static poses to movements, without being affected by the angle of view.
-
A demonstration of how the learned basis poses can be used in various applications, including manifold traversal, discriminative classification, and synthesis of movements.
-
The introduction of three new sets of annotations for each image in the LSP dataset. (1) The ground truth sport label that each portrayed person is performing, (Athletics, Badminton, Baseball, Gymnastics, Parkour, Soccer, Tennis, Volleyball, Other). (2) The mean and variance for the angle of view that each portrayed person is facing, obtained by three different annotators. (3) The 3D pose of each portrayed person, obtained through the MPI Pose Prior algorithm. See the Dataset section for more details.
Results
We analyze the flexibility and usefuleness of the proposed model in a variety of application domains and experiments. In particular, we evaluate (i) the performance of the learned representation for supervised learning tasks such as activity classification; (ii) whether the learned representation captures enough semantics for meaningful manifold traversal and visualization; and (iii) the robustness to initialization and the generalization error. Finally, we provide a qualitative visualization of the embedding of the manifold of human motion that was learned. Collectively, results suggest that our approach is effective at capturing rotation invariant semantics of the underlying data.
Activity Recognition
Action Dynamics Inference
Moveme Visualization
Initialization Sensitivity
Manifold Visualization
- Dataset Version [1.0]: 2000 images with corresponding 2d and 3d keypoint locations for 14 joints of the human body, activity and angle of view annotations.
- If you use the data provided at this page please cite our work along with the following two references.
- [1] Leeds Sports Pose Dataset
- [2] Pose Prior 2D to 3D Toolbox
- This data is licensed under the Simplified BSD License.
- Code Version [1.0.0].
- This code and data are licensed under the Simplified BSD License.
-
A Rotation Invariant Latent Factor Model for Moveme Discovery from Static Pose
M.R. Ronchi, J.S. Kim and Y. Yue
ICDM 2016, Barcelona, Spain, December 2016.
Bibtex Long Paper Short Paper Poster Presentation
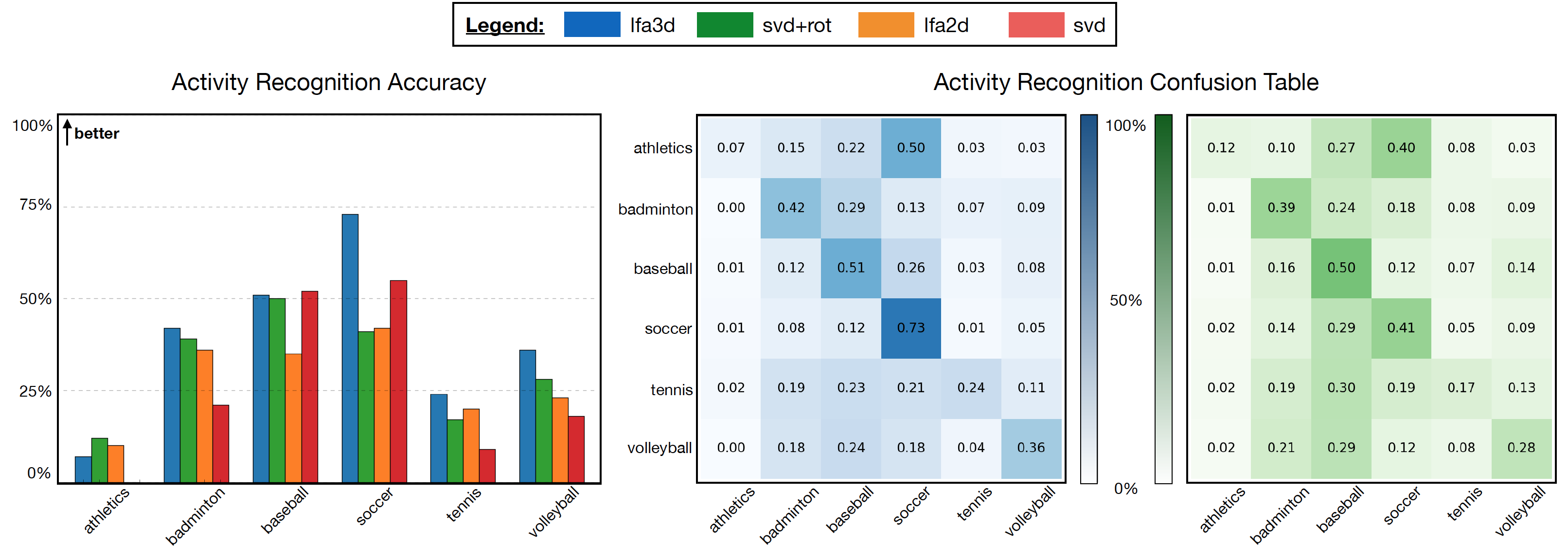
We show the results obtained from five fold cross validation. The proposed 3-D latent factor model (lfa3d) outperforms all other methods by an average accuracy of about 11%. The 2-D model (lfa2d) performs slightly worse than the clustered SVD baseline (svd+rot), but both show more than a 5% average improvement over the svd baseline.
The two most challenging activities are athletics, which does not posses characterizing movements; and tennis, whose movemes are shared and thus confused with multiple other sports, badminton and baseball above all.
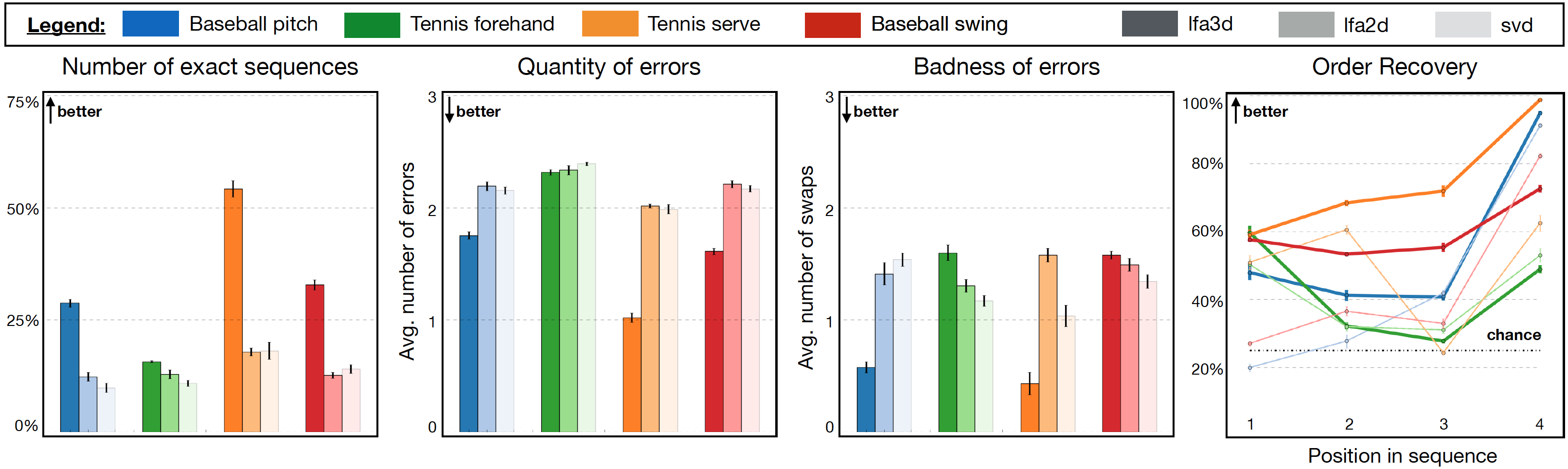
In this experiment, we shuffled 1000 sequences of four images for four sport actions (baseball pitch, tennis forehand, tennis serve, baseball swing), and verified how precisely could the underlying chronological sequence be recovered. The analysis is repeated five times to obtain standard deviations, and performance is measured in terms of three metrics (shown in the figure): (1) what percentage of the 1000 sequences is exactly reordered; (2) how many poses are wrongly positioned; and (3) how bad are the reordering mistakes, computed as the number of swaps necessary to correct a sequence. We also plot the per-position accuracy in each sport for all methods.
The lfa3d model has significantly better outcomes compared to lfa2d and svd, which perform similarly. Specifically, lfa3d correctly reorders more than twice the sequences overall (1314 against 555 of lfa2d) averages 1.6 errors, and is the only algorithm to require an average number of swaps smaller than 1.
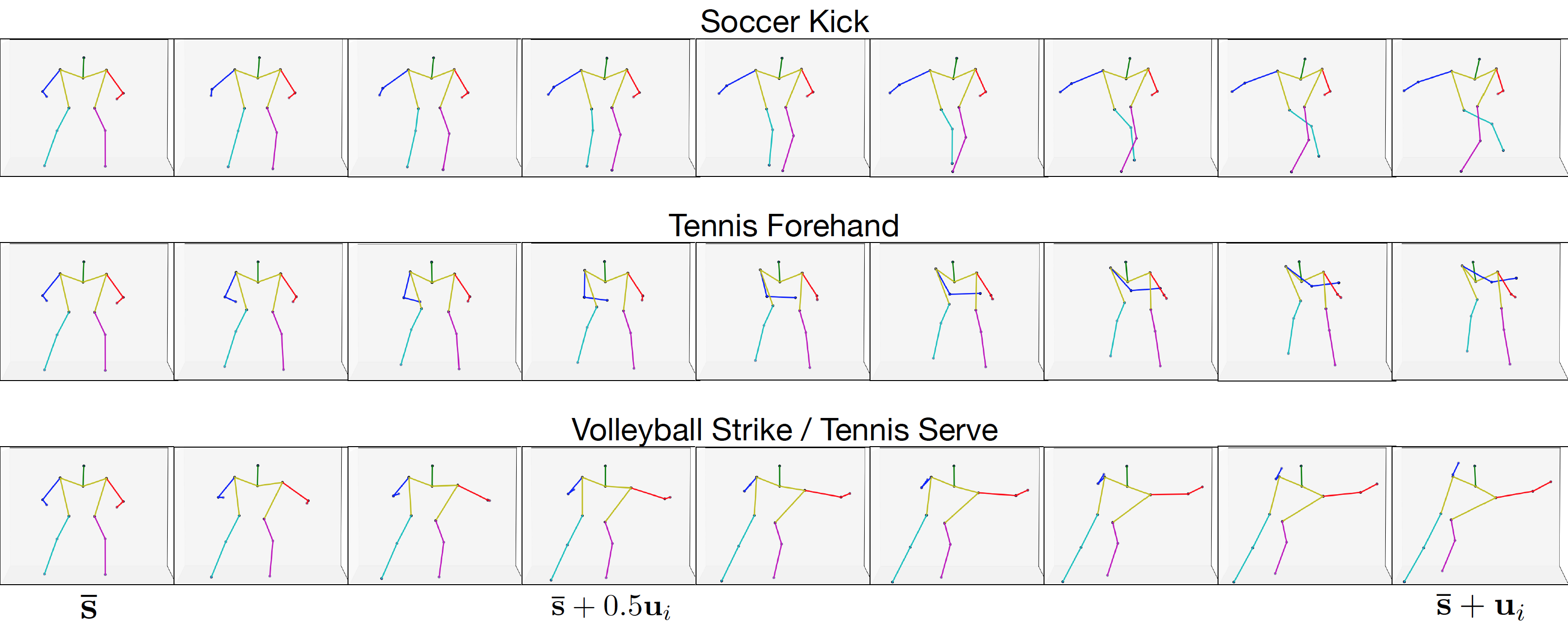
The most significant movemes contained in the training set are captured by the basis pose matrix U and encoded in the form of a displacement from the mean pose. Each column of U corresponds to a latent factor that describes some of the movement variability present in the data.
We report the motion described by three latent factors: the rows show the pose obtained by adding an increasing portion of the learned moveme (from 30% - second column, to 100% - last column) to the mean pose of the data (first column). Two are easily interpretable, soccer kick and tennis forehand, while one is not as well defined, volleyball strike / tennis serve. The movemes differentiate very quickly, as early as 50% of the final movement is added.
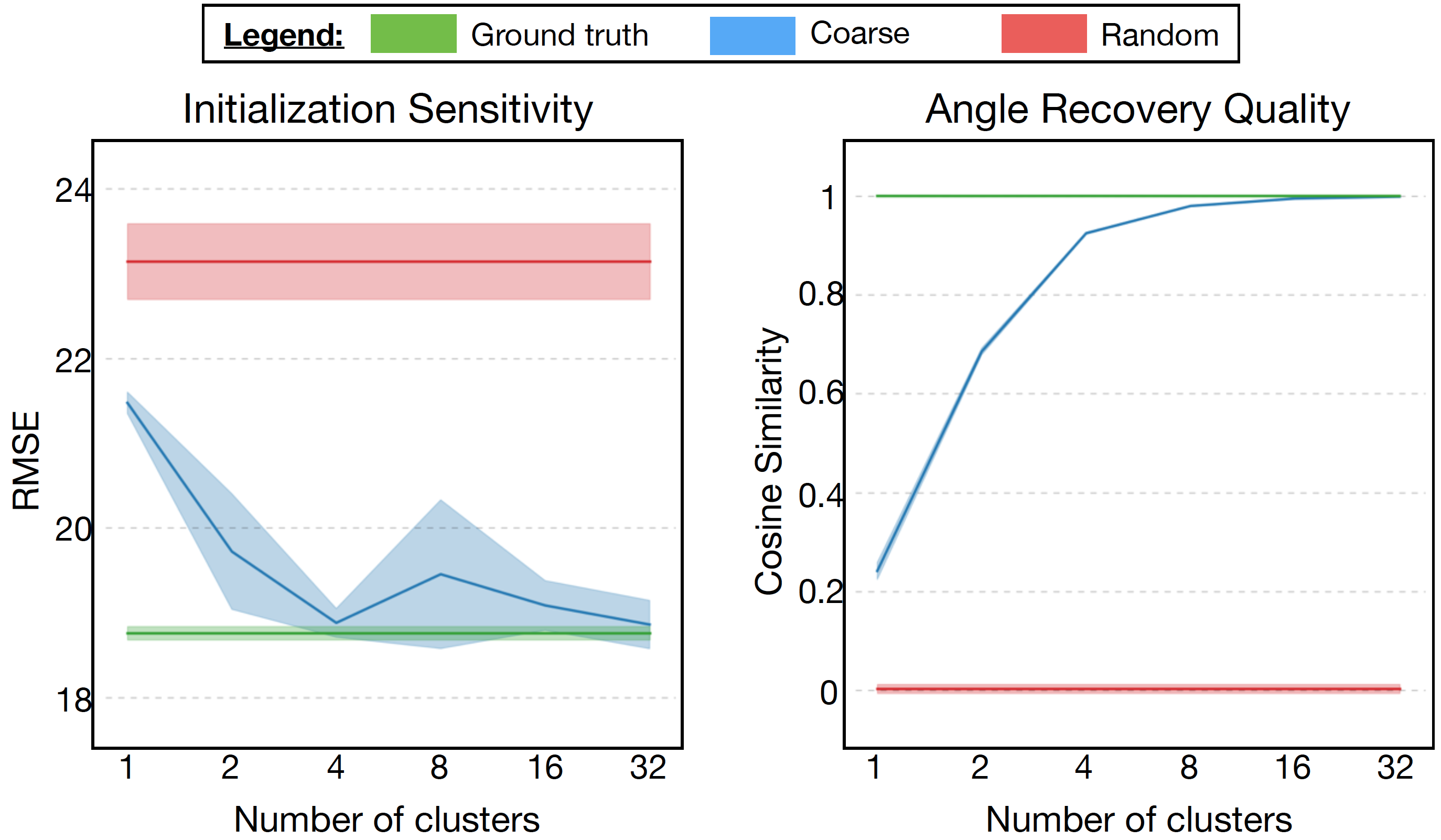
The lfa3d method learns a rotation invariant representation by treating the angle of view of each pose as a variable which is optimized through gradient descent, and requires an initial guess for each training instance. We investigate how sensitive is the model to initialization, and how close is the recovered angle of view to the ground truth.
In the above Figure, we show the Root Mean Squared Error (RMSE) and cosine similarity with ground truth, for three initialization methods: (1) random, between 0 and 2π; (2) coarse, coarsening into discrete buckets (e.g., 4 clusters indicates that we only know the viewing angle quadrant during initalization); and (3) ground-truth.
As the number of clusters increases, we see that performance remains constant for random and ground truth, while both evaluation metrics improve significantly for coarse initialization. For instance, using just four clusters, coarse initialization obtains almost perfect cosine similarity. These results suggest that using very simple heuristics to predict the viewing angle quadrant of a pose is sufficient to obtain optimal performance.

Each pose in LSP is mapped in the human motion space through the coefficients of the corresponding column of V learned with the lfa3d method, and then projected in two-dimensions using t-SNE. Poses describing similar movements are mapped to nearby positions and form consistent clusters, whose relative distance depends on which latent factors are used to reconstruct the contained poses. Upper body movements are mapped closely in the lower right corner, while lower body movements appear at the opposite end of the embedding. The mapping in the manifold is not affected by the direction each pose is facing, as nearby elements may have very different angle of view, confirming that the learned representation is rotation invariant.
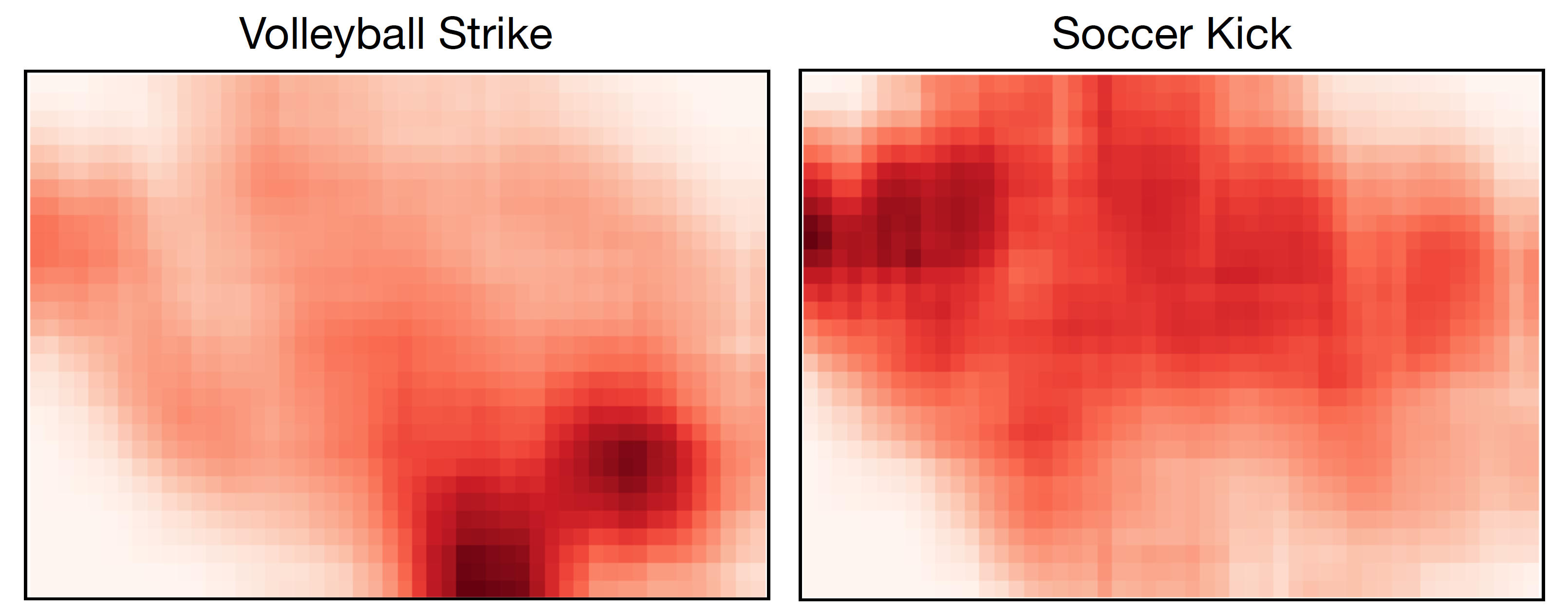
The heatmaps obtained from the activations of two latent factors (soccer kick and volleyball strike), overlaid on top of the t-SNE mapping are shown in the Figure on the left. Clearly, the epicentrum of the volleyball strike basis pose is located where volleyball-like poses appear in the t-SNE plot (lower-right corner). Conversly, the soccer kick basis pose is mostly dominant in the top-left area and the heatmap is diffused, consistent with the observation that most poses contain some movement of the legs.
Comprehensive LSP (CO_LSP) Dataset
We extended the LSP dataset, providing additional annotations of the angle of view each depicted subject is facing. We also include the 3D keypoint locations of the 14 joints of the human body, obtained by runnnig an off-the-shelf method for 2D to 3D pose estimation algorithm [2], along with the 2D annotations from the original LSP dataset [1]. We redistribute these comprehensive annotations in JSON format as the Comprehensive LSP (CO_LSP) Dataset, along with a Python API to load, manipulate and visualize the annotations.
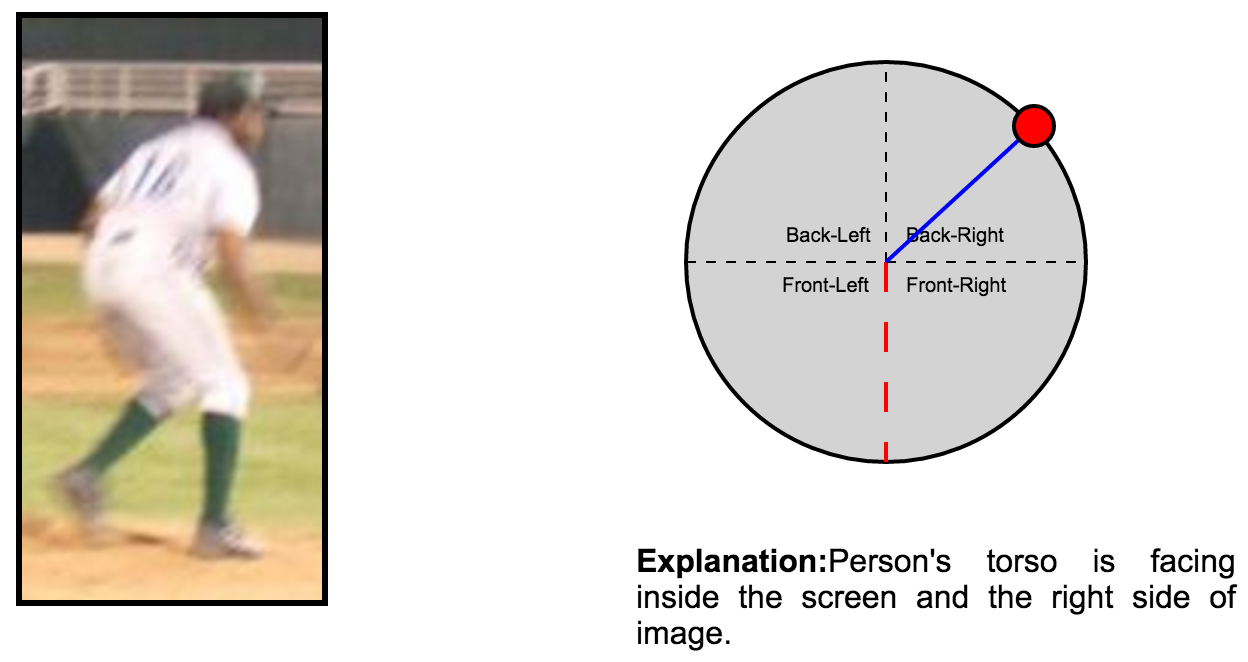
We collected high-quality viewing angle annotations for each pose in LSP. Although these annotations are not necessary for training, we used them to demonstrate the robustness of our model to poor angle initialization, and that it can in fact recover the ground truth value. Three annotators evaluated each image and were instructed to provide the direction at which the torso of the depicted subject was facing through the GUI visible in Figure. The standard deviation in the reported angle of view averaged over the whole dataset is 12 degrees, and more than half of the images have a deviation of less than 10 degrees, showing a very high annotator agreement for the task.
Example visualization for an annotation in the dataset:
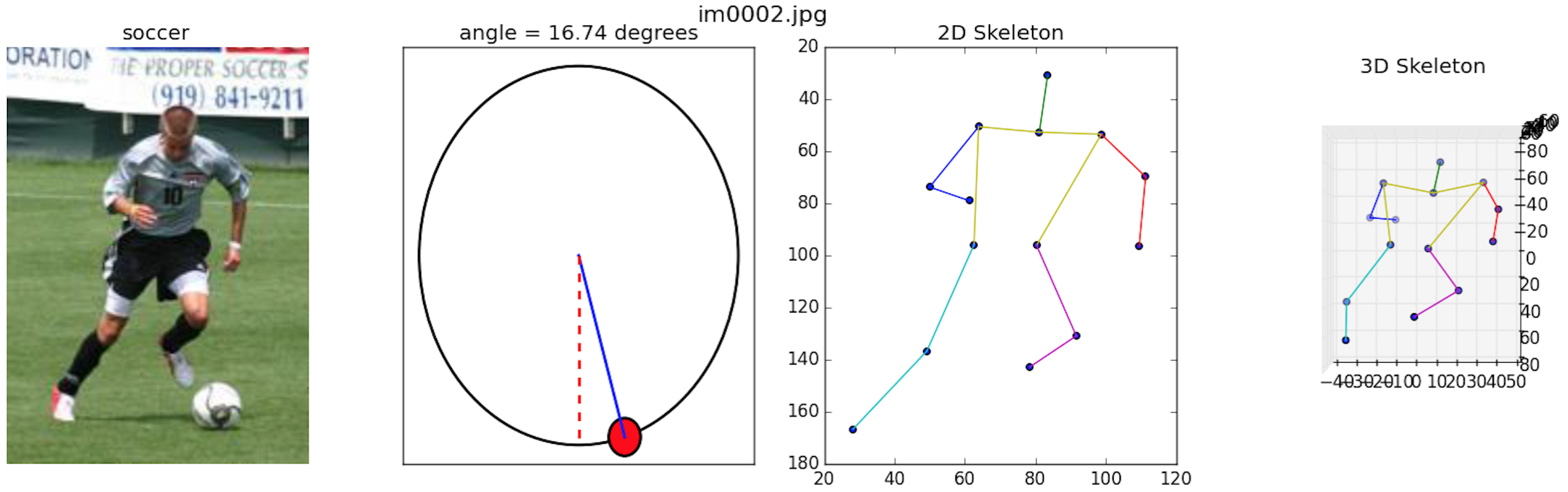
Download
We provide a python implementation of our algorithm and the three new annotations of the LSP dataset in JSON file format. Full details are described in the Dataset Section and in the README files.
Notes:Cite
If you find our paper or the released data or code useful to your work, please cite:
@inproceedings{ DBLP:conf/icdm/RonchiKY16, author = {Matteo Ruggero Ronchi and Joon Sik Kim and Yisong Yue}, title = {A Rotation Invariant Latent Factor Model for Moveme Discovery from Static Poses}, booktitle = {IEEE 16th International Conference on Data Mining, {ICDM} 2016, December 12-15, 2016, Barcelona, Spain}, pages = {1179--1184}, year = {2016}, crossref = {DBLP:conf/icdm/2016}, url = {https://doi.org/10.1109/ICDM.2016.0156}, doi = {10.1109/ICDM.2016.0156}, timestamp = {Mon, 11 Feb 2019 17:32:48 +0100}, biburl = {https://dblp.org/rec/bib/conf/icdm/RonchiKY16}, bibsource = {dblp computer science bibliography, https://dblp.org}}